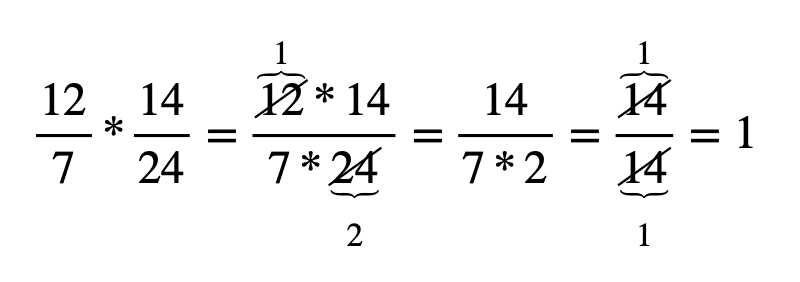➗ Zlomky #7
Každý môže vedieť so zlomkami narábať. Už od škôlky si vieme spravodlivo rozdeliť medzi sebou cukríky. Tak prečo robia taký problém v neskoršom veku? Tento list ti chce pomôcť im porozumieť.
Ako chápať zlomok
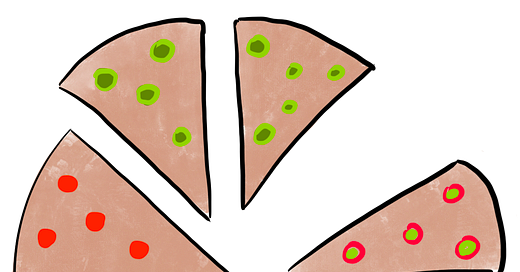
Zlomok je časť celku. Môže to byť aj celok sám. Jedna polovica, tretina, tri osminy, dve celé, a podobne. Predstav si to ako pizzu rozdelenú na osminky. Jedna osminka, to je zlomok. Aby sme v matematike nemuseli písať výrazy slovom ako na slovenčine, máme na to symbolický zápis:
Skús si všimnúť, keď bude mama alebo babička krájať koláč, akú časť z neho dostaneš. Nakrája ho na plechu na 20 kociek? Na 30 kociek? Koľko z nich dostaneš k čaju, mlieku alebo len tak? Ak dostaneš na tanierik 5 kociek z 20, dostala si zlomok päť dvadsatín, zapísaný symbolicky:
Päť kociek z dvadsiatich je štvrtina celého koláča, preto môžeme tvrdiť, že:
To je zlomok. Časť celku alebo aj celok sám. Kým prejdeme na niekoľko matmatických konštrukcií, vráťme sa trochu do histórie symbolu delenia.
Prečo toľko symbolov (/ : ÷) pre delenie?
Niekde sa píše lomítko, niekde dvojbodka, inde dvojbodka s čiarkou medzi nimi a samotný zlomok sa píše s vodorovnou čiarou medzi číslami. Jeden zlomok a štyri rôzne formy zápisu:
Dôvodom je historická tradícia. Kým v Európe sa ako delenie používala dvojbodka (:), v arabskom svete to bola horizotnálna (–) alebo lomená (/) čiara. Keď sa stretli európska dvojbodka s arabskou čiarkou, boli skombinované do jedného symbolu delenia (÷), ktorý používame dodnes na kalkulačkách.
Dnes väčšinou používame kalkulačky, počítače či mobily na to, aby sme vydelili dve čísla medzi sebou. Schopnosť počítať so zlomkami však patrí k matematickému umeniu, ktoré pomáha tvojmu mozgu 🧠 rásť. Nie preto, že by sa nezmestil do tvojej hlavy, ale čo sa týka počtu neurónových prepojení. Čím viac prepojení, tým lepšie vieš riešiť akékoľvek problémy.
Sčitovanie a odčitovanie
Chápať princíp zlomku je ľahké. To zvládajú už škôlkári, keď si medzi sebou delia cukríky. Čo je ťažšie, no zároveň pochopiteľné, je ich sčitovanie (súčet) a odčitovanie (rozdiel). Obidve operácie sa dajú chápať ako súčet. Buď pripočítavame kladný zlomok, alebo pripočítavame záporný zlomok.
Ak majú dva zlomky to isté číslo pod čiarou, v menovateli, súčet je ľahký:
Dve osminy a tri osminy, dve a tri, to je dokopy päť. Päť osmín.
Stačí sčítať čitatele, tie čísla hore. Menovateľa ponecháme tak, ako je. Obrázok vyššie to ilustruje ešte jasnejšie.
Čo sa stane, ak sa kuchár zabudne a nakrája prvú pizzu na štvrtiny a druhú na šestiny? Ako vyjadríme časť celku, ak chceme povedať, že sme z prvej pizze zjedli tri štvrtiny a z druhej päť šestín? Koľko sme zjedli spolu z obidvoch pízz?
Matematickým jazykom sa opýtame toto:
Obidva zlomky musíme dať na spoločného menovateľa. Musia mať to isté číslo pod zlomkovou čiarou.
Ako? Buď hľadáme najmenší spoločný násobok menovateľov (nsn, lcm), alebo menovatele medzi sebou vynásobíme. Tá druhá možnosť je jednoduchšia. Operácia sa opisuje aj ako operácia nič. To preto, lebo oba zlomky najskôr prenásobíme jednotkami. Aha:
Povieš si, na čo je dobré také prenásobenie, ktoré naozaj urobí nič? Trik je v tom, čomu sa tie jednotky môžu rovnať:
Ako môžeš vidieť, tri štrtiny sme prenásobili šiestimi šestinami. Jednotkou. Šestka je číslo z menovateľa druhého zlomku. A zlomok päť šestín sme prenásobili štyrmi štvrtinami. Znovu jednotkou. Štvorka je číslo z menovateľa prvého zlomku. Keďže máme v menovateľoch oboch zlomkov to isté číslo (spoločného menovateľa 4*6), môžeme ich dať do jedného zlomku pomocou jednej zlomkovej čiary takto:
To je už len kúsok od výsledku. Stačí všetko spočítať:
Tým pádom môžeme tvrdiť, že z oboch pízz sme dohromady zjedli devätnásť dvanástin. To je viac, ako jedna pizza.
Keď chceme dva zlomky od seba odčítať, je to presne tento istý postup, ako sčítanie. Žiaden rozdiel v tom nie je, okrem znamienka:
Teda keď od piatich šestín odpočítame dve tretiny, získame jednu šestinu. Jednoduché, že? 😉
Existuje aj schéma, nazývaná motýlik, ktorá toto celé jednoducho znázorňuje:
Vyznač si krížom hodnoty z oboch zlomkov. To značí násobenie. Následne čitateľ nového zlomku vznikne spočítaním týchto násobkov. Menovateľ nového zlomku vznikne vynásobením menovateľov pôvodných zlomkov.
To je celé k sčitovaniu.
Násobenie
Násobenie zlomkov je veľmi jednoduché. Stačí medzi sebou vynásobiť pôvodné čitatele a výsledok dať do čitateľa nového zlomku a potom vynásobiť pôvodné menovatele a výsledok dať do menovateľa nového zlomku. Na nasledujúcom príklade pozoruj jednotlivé čísla:
Schematicky je možné násobenie vnímať takto:
Ak si to chceš predstaviť, urob si obdĺžnik. Z jednej strany ho rozdeľ na štyri rovnaké časti (štvrtiny) a vyfarbi len tri z nich (tri štvrtiny). Z druhej strany ho rozdeľ na sedem rovnakých častí (sedminy), vyfarbi päť z nich (päť sedmín). Vznikla čokoládka, ktorá je vyfarbená dvomi farbami. Výsledný zlomok je tá časť, ktorá obsahuje obe farby z celkovej plochy.
Teraz spočítaj počet tabličiek celej čokoládky (28), to je menovateľ, a spočítaj počet tabličiek vyfarbených obomi farbami (15), to je čitateľ.
Delenie
Delenie vyžaduje jeden trik, preto sa mu povenujeme samostatne.
Majme dva zlomky, ktoré chceme medzi sebou vydeliť:
Trik je v tom, že druhý zlomok musíme prevrátiť:
Teraz stačí správne krátiť hodnoty medzi čitateľom a menovateľom:
Prečo to tak je? Ako je možné, že delenie sa dá prerobiť na násobenie? Ukážme si. Najskôr si prepíšme podiel zlomkov do jedného, zloženého zlomku:
V ďalšej operácii veľký zlomok prenásobíme jednotkou, čo v matematike nazývame operácia nič. Túto jednotku následne napíšeme ako zlomok vytvorený z obráteného zlomku z menovateľa. Prečo? Lebo môžeme a bude sa to hodiť:
Táto operácia nič nám pomôže zjednodušiť menovateľ veľkého zlomku natoľko, že v podstate úplne zmizne:
Lebo sme použili logické matematické operácie, získali sme tú istú hodnotu, ako má pôvodný výraz. Preto môžeme tvrdiť, že ak delíme dva zlomky medzi sebou, ten druhý otočíme a delenie zmeníme na násobenie:
Spoločný menovateľ
Spoločný menovateľ sme si spomenuli v časti, kde sme dva zlomky sčitovali. Bolo by zbytočné tento postup znovu opakovať. Preto si to predstavme vo všeobecnosti, pomocou písmen.
Ďať dva zlomky na spoločný menovateľ znamená, že robíš túto operáciu:
Alebo na to použi schému motýlik:
Záver
Verím, že ti prečítané informácie dodajú trochu svetla do zlomkov a ich fungovania. Lebo zlomky nie sú zložitý matematický koncept. Dôležité je pochopiť, ako sa s nimi narába a prečo to tak je. Tak sa nad tým dobre zamysli a precvič si to na niekoľkých príkladoch.
Zdroje
Zdroje, odkiaľ čerpá informácie tento list: