🐇 Páriace sa králiky #4
Ako sa množia králiky? Leonardo z Pisy, známy pod menom Fibonacci, opísal v roku 1202 množenie sa králikov za nerealisticky ideálnych podmienok.
Ako to už ale vo svete matematiky býva, nerealisticky (hlavne z pohľadu biológie) nastavené podmienky zjednodušujú vnímanie reality okolo nás, čo zjednodušuje skúmanie, čo potom vedie k dômyselným poznatkom aplikovateľných inde, aj do neideálnych podmienok. Poďme sa teda na tie králiky pozrieť pod drobnohľadom.
Podmienky matematického modelu králikov sú tieto:
Jeden pár čerstvo narodených králikov (samicu, samca) dáme dohromady 🐇+🐇=❤️;
Králiky sú schopné páriť sa po uplynutí jedného mesiaca od narodenia. Po uplynutí druhého mesiaca porodí samica nový pár králikov (samicu, samca);
Králiky nikdy nezomrú a páriaci sa pár vždy privedie na svet nový pár králikov (jednu samicu, jedného samca) každý mesiac po mesiaci.
Otázka (stará vyše 800 rokov) od Fibonacciho znie:
Koľko párov králikov budeme mať po jednom roku?
Najskôr sa zamysli nad tým ty, odlož tento list nabok, porozmýšľaj, kresli a po jednom celom dni sa vráť a čítaj ďalej.
❀ PAUZA 1 DEŇ ❀
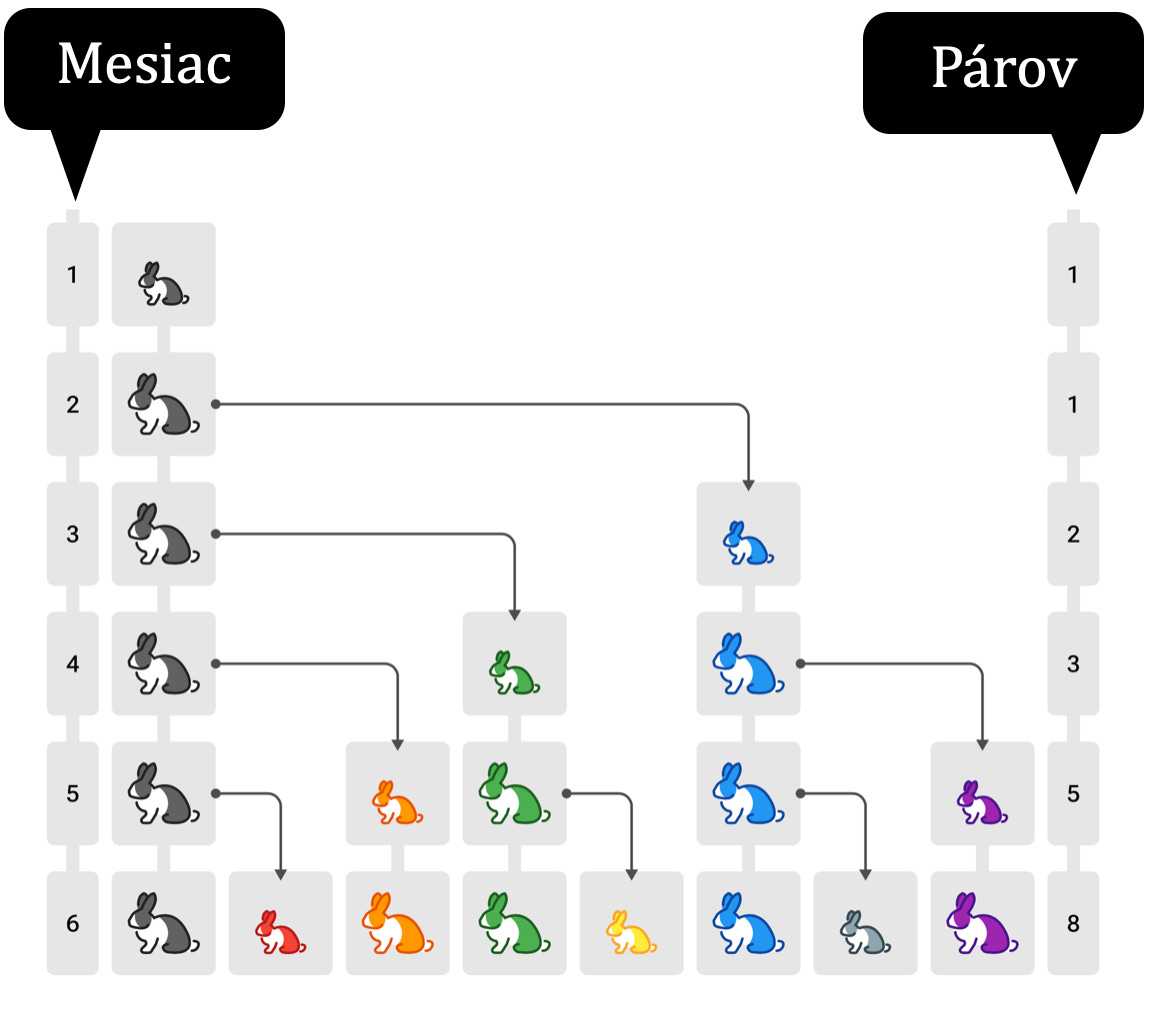
V zásade všetko sa dá vyriešiť krásnym obrázkom. Aha:
Fibonacci si všimol skutočnosť, že každý ďalší mesiac bude toľko párov králikov, koľko bolo mesiac dozadu plus dva mesiace dozadu. Tým pádom sa dá dedukovať nové množstvo králikov len matematickým modelom bez simulácie v realite.
Keď si zapíšeme počty párov králikov za sebou, získame túto postupnosť čísel:
Táto postupnosť sa na počesť svojho objaviteľa volá Fibonacciho postupnosť. Funguje tak, že každé nové číslo postupnosti bude súčtom dvoch predchádzajúcich. Tvojou úlohou je niekde na blízky papier napísať číslo, ktoré bude nasledovať hneď za číslom 55. Ak sa chceš pochváliť svojimi znalosťami, kľudne mi pošli email. ✉️
Príklad s králikmi je umelý, no časom sme prišli na to, že Fibonacciho princíp sa vyskytuje aj inde. Pozrieme sa na pár skutočností, ktoré sú touto postupnosťou dobre popísateľné. Najskôr si ale dáme matematický model, nech máš čo počítať. Ako postupne zistíš, je to úplne jednoduché.
Matematický model
Princíp Fibonacciho postupnosti je v tom, že začíname s dvomi štartovacími číslami 0 a 1. Každé ďalšie sa generuje ako súčet dvoch predchádzajúcich:
0+1=1
1+1=2
1+2=3
2+3=5
3+5=8
…
Zvyšné čísla už vieš spočítať hravo. Skús výpočty doplniť, ako by pokračovali na ďalších riadkoch. Poďme sa pozrieť na výskyt týchto čísel v divočine.
Koberčeky
Skúsme najskôr ukladať vedľa seba štvorcové koberčeky. Čo keby každý z nich mal plôšku inšpirovanú Fibonacciho číslami? Obrázok asi napovie viac.
Zaujímavosťou je, že každý ďalší väčší štvorček, ktorý pridáš, je ďalšie číslo z postupnosti, o ktorej sa tu bavíme. Teda dĺžky jeho strány. Žiadny nebude vybočovať z rady. Prečo to tak pekne na seba nadväzuje? Uvažovanie nechám na teba. Isto na to prídeš.
Ruka a predpovede
Veľmi podobný obrázok získame, ak odmeriame proporcie ruky. Prvý článok ukazováka ruky dospeláka je dlhý 2 cm, druhý je dlhý 3 cm, tretí je dlhý 5 cm a vzdialenosť základných kĺbov ukazováka a palca je 8 cm. To sú presne čísla z Fibonacciho postupnosti. Je zrejmé, že tieto hodnoty nebudú rovnaké u každého, ale ich vzájomný pomer bude veľmi blízky pomerom pôvodných čísel.
Prečo to tak je? Sú tieto čísla v prírode výhodnejšie, ako iné? Zdá sa, že áno. Ak budeme uvažovať v intenciách ľudskej ruky, odpoveďou môže byť, že dôvod na tieto proporcie je, aby sa ruka dokázala do seba perfektne uzavrieť. Ešte raz sa dobre pozri na koberčeky vyššie a zistíš, že súčet predchádzajúcich dvoch strán je dĺžka väčšej nasledujúcej. Teda dve predchádzajúce dĺžky sú v dokonalom zákryte za väčšou časťou.
Niekto môže mať tieto rozmery menšie, niekto väčšie. Ide však o ich vzájomný pomer. Ak je pomer prvých dvoch čísel 2:3, tak taký istý bude mať každý človek. Pomer 3:5 bude tiež rovnaký pre všetkých a rovnako aj 5:8. Malé odchýlky sa môžu vyskytnúť, ale štatisticky to bude veľmi blízko týchto hodnôt.
Ak bude mať niekto prvý článok ukazováka dlhý 1,5 cm, potom druhý článok spĺňajúci pomer 2:3 bude mať dĺžku 2,25 cm. Takto si vieš spočítať predpoveď dĺžok pre jednotlivé proporcie dopredu bez toho, aby si ich musela merať.
Matematika dovoľuje týmto spôsobom robiť predpovede toho, o čom ešte nič nevieme. Vieš robiť objavy, rozhodnutia, odhady.
Špirála
Keď si všimneš zavretú ruku alebo koberčeky, tak dané proporcie vytvárajú tzv. Fibonacciho špirálu, ktorá sa vyskytuje všelikde v prírode. A môžeme sa domnievať, že je to práve z dôvodu ľahkej „uložiteľnosti“, optimálnosti usporiadania.
Nautilus, alebo aj lodička, je krásnym príkladom tohto usporiadania. Keď si dobre pozrieš vnútorný prierez schránky tohto živočícha, tak uvidíš jej vnútornú matematickú krásu.


Rovnako tento špirálovitý princíp pozorujeme aj v rozrastajúcich sa púčikoch rastlín. Skús nájsť ty výskyt podobného tvaru inde v prírode a pošli mi email. 😉
Šuška
Špirály sú častým javom v prírode, ale i vo vesmíre. Jedným z ďalších výskytov špirál okolo nás sú šušky. Najlepšie to vidno na borovicových. Nejedná sa však o Fibonacciho špirálu s proporciami, o ktorých rozprávame vyššie, tentoraz ide o počet špirál, ktoré vytvárajú šupiny.


Nie sú to náhodou čísla z Fibonacciho postupnosti, ktoré vyjadrujú počet špirál jedným alebo druhým smerom?
Zlatý pomer
Isto si dakedy počula o zlatom pomere. Bájne číslo označené gréckym písmenom fí:
Jeho výskyt odhalíme práve vo Fibonacciho postupnosti. Urobme zlomky z jednotlivých za sebou idúcich dvojíc postupnosti takto:
Čím viac budeme pokračovať hlbšie do postupnosti, tým bližšie bude daný zlomok k zlatému pomeru. Prečo to tak je? Vysvetliť to matematicky je jednoduché, ale prečo je zlatý pomer ukrytý práve vo Fibonacciho postupnosti a nie inej? To nechám tvojej zvedavosti.
Zlomky z Pisy
Urobme zlomky z tejto postupnosti, no v opačnom poradí, ako predtým. Do čitateľa dajme jedno (hocijaké) číslo a do menovateľa dajme nasledujúce (to väčšie). Napríklad:
Zaujímavosťou je, že každý z týchto zlomkov sa dá zapísať ako reťazový zlomok použitím iba samých jednotiek:
alebo
Vieš vytvoriť dáke ďalšie? Ak áno, skús si dať pauzu v čítaní a nejaké zapísať perom 🖋 na papier 📃.
Záver
🤔 No nie je to úžasné, ako páriace sa králiky môžu súvisieť s reťazovými zlomkami zloženými iba zo samých jednotiek? Nie je fascinujúce, ako súvisia páriace sa králiky s tým, ako evolúcia zabezpečila konštrukciu organizmov? Matematika obsahuje mnoho zákutí, na ktoré ešte nepoznáme odpovede. Práve preto je tak krásne ich hľadať.
Zdroje
Zdroje, odkiaľ čerpá informácie tento list:
https://en.wikipedia.org/wiki/Fibonacci_number (odtiaľto je aj obrázok koberčekov)
https://commons.wikimedia.org/wiki/File:Fibonacci_Rabbits.svg (zajkovia)
🧠 Matematická omaľovánka
Matematika je hlavne o schopnosti hľadať vzory (ang. patterny). Nenájdeš ich, ak budeš vedieť len počítať, musíš vedieť aktívne pracovať s otázkami a odpoveďami na ne. Mohlo by sa zdať, že obyčajné vyfarbovanie obrázkov nedáva zmysel. Pravdou však je, že svoj mozog 🧠 trénuješ na to, aby ľahšie hľadať vzory aj medzi číslami a vzorčekmi. Lebo je preukázané, že ak pracuješ s matematikou aj vizuálne, dokážeš ju pochopiť lepšie.
Pre prístup k matematickej omaľovánke má podpor formou plateného prístupu. Pomôžeš mi tak rozširovať povedomie o matike.
Keep reading with a 7-day free trial
Subscribe to Matematické listy to keep reading this post and get 7 days of free access to the full post archives.